rules = {'A': '[>FA][^FA]'}
axiom = 'FA'
n_iters = 2
seq = [''.join([rules.get(c,c)
for c in (locals()['_[1]'][-1] if locals()['_[1]'] else axiom)]) for i in range(n_iters)][-1]
print seq # F[>F[>FA][^FA]][^F[>FA][^FA]]
seq = axiom for i in range(n_iters): rewrite = '' for c in seq: rewrite += rules.get(c, c) seq = rewrite print seq # F[>F[>FA][^FA]][^F[>FA][^FA]]
from numpy import * class Turtle: def __init__(self): self.T = eye(4) # transformation matrix self.stack = [] def getPos(self): return array([self.T[0][-1], self.T[1][-1], self.T[2][-1]]) def getDir(self): return dot(self.T, [0, 1, 0, 0])[:3] def rotateX(self, a): self.T = dot(self.T, [[1, 0, 0, 0], [0, cos(a), -sin(a), 0], [0, sin(a), cos(a), 0], [0, 0, 0, 1]]) def rotateY(self, a): self.T = dot(self.T, [[cos(a), 0, sin(a), 0], [0, 1, 0, 0], [-sin(a), 0, cos(a), 0], [0, 0, 0, 1]]) def rotateZ(self, a): self.T = dot(self.T, [[cos(a), -sin(a), 0, 0], [sin(a), cos(a), 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]]) def translate(self, d): self.T += [[0, 0, 0, d[0]], [0, 0, 0, d[1]], [0, 0, 0, d[2]], [0, 0, 0, 0 ]] def forward(self, d=1): self.translate(self.getDir() * d) def pushMatrix(self): self.stack.append(self.T.copy()) # copy is important! def popMatrix(self): self.T = self.stack.pop()
F character, as the rest can be handled by our turtle:
from visual import * turtle = Turtle() angle = radians(30) for c in seq: if c == 'F': cylinder(pos=turtle.getPos(), axis=turtle.getDir(), radius=0.1) turtle.forward() elif c in '^v': turtle.rotateX(angle if c == 'v' else -angle) elif c in '+-': turtle.rotateY(angle if c == '+' else -angle) elif c in '<>': turtle.rotateZ(angle if c == '>' else -angle) elif c == '[': turtle.pushMatrix() elif c == ']': turtle.popMatrix()
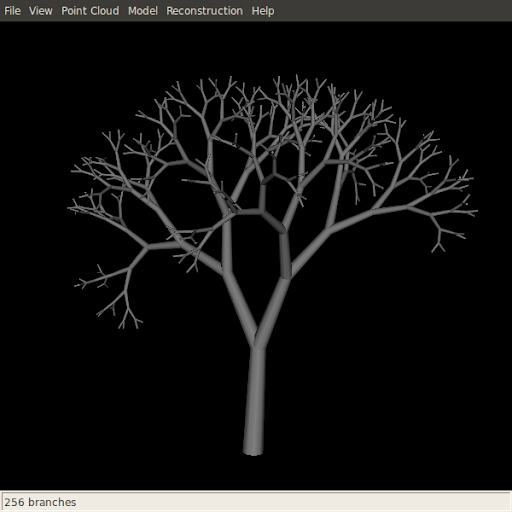
Actually.. I cheated a little for this picture: I did not generate it using VPython, but rather with the Python bindings for VTK, a truly powerful toolkit, that I strongly recommend for any scientific visualization need.
There's a nice and freely available book about this very rich topic, co-written by its pioneer, Aristid Lindenmayer.