Problem Representation
The first task is working up the problem representation. We need to parse:
s = """|de| | f|Cl|nf|ed|au| i|ti| |ma|ha|or|nn|ou| S|on|nd|on|
|ry| |is|th|is| b|eo|as| | |f |wh| o|ic| t|, | |he|h |
|ab| |la|pr|od|ge|ob| m|an| |s |is|el|ti|ng|il|d |ua|c |
|he| |ea|of|ho| m| t|et|ha| | t|od|ds|e |ki| c|t |ng|br|
|wo|m,|to|yo|hi|ve|u | t|ob| |pr|d |s |us| s|ul|le|ol|e |
| t|ca| t|wi| M|d |th|"A|ma|l |he| p|at|ap|it|he|ti|le|er|
|ry|d |un|Th|" |io|eo|n,|is| |bl|f |pu|Co|ic| o|he|at|mm|
|hi| | |in| | | t| | | | |ye| |ar| |s | | |. |"""
grid = [[''] * 8 for i in range(19)] for j, line in enumerate(s.split('\n')): cols = line.strip().split('|')[1:-1] for i, col in enumerate(cols): grid[i][j] = col
def repr(grid): return '\n'.join(['|%s|' % '|'.join([grid[i][j] for i in range(19)]) for j in range(8)])
State Space Exploration
For the exploration function, here is a simple approach: from a given grid configuration, consider all the possible grid reorderings, resulting from having an arbitrary column reinserted to an arbitrary position. Then expand them in the order of their score ranking. Here is an example showing two possible column reorderings from the initial state: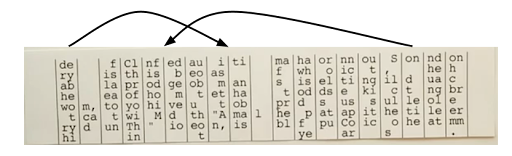
def nextGrids(grid): global visited # I know.. next_grids = set() for i in range(19): for j in range(19): if i == j: continue next_grid = list(list(col) for col in grid) next_grid.insert(i, next_grid.pop(j)) next_grid = tuple(tuple(col) for col in next_grid) if next_grid not in visited: next_grids.add(next_grid) return next_grids
sets to avoid repetitions (both for the already explored states overall and the reinsertion configs for a given grid), which thus requires those ugly "tuplify/listify" operations (a list is editable but not hashable, while a set is the opposite). We can then use this function in a greedy and heuristic way, always expanding first the best reordering from any given state (using a heap to make our life easier):
visited = set() frontier = [] # heap of (score, grid)'s while True: for next_grid in nextGrids(grid): # using a min-heap so score has to be negated heappush(frontier, (-gridScore(next_grid), next_grid)) score, grid = heappop(frontier) visited.add(grid) score, grid = max(results) print repr(grid) print score
Some Doubts..
At first, my solution wasn't based on a heap: it was simply considering the best configuration at any point, and then would forget about the others (in other words: it used a single-element search frontier). But I had doubts: was this strategy guaranteed to eventually exhaust the space of the possible permutations of a given set? If not, even in theory, it would seem to be a potential problem as for the generalness of the solution.. I'm not sure about the math required to describe the relationship between the n! permutations of a set and the n2-2n+1 element reorderings (there must be a technical term for this?) from any configuration, but after having performed some practical tests, I reached the conclusion that using a heap-based method (i.e. a frontier with many elements) was more sound, because although I cannot prove it, I'm pretty certain that it is guaranteed to eventually exhaust the permutation space, whereas the first method is not. In the context of this problem, it doesn't make a difference though, because the search space is so large that we would have to wait a very long time before we see these two closely related strategies behave differently.Language Modeling
Enters language modeling.. this is the component we need for the evalution function, to tell us if we are heading in the right direction or not, in terms of unscrambling the hidden message. My first intuition was that character-based n-grams would work best. Why? Because while exploring the state space, due to the problem definition, most of the time we are dealing with parts or scrambled words, not complete (i.e. real) ones. Thus a character-based n-gram should be able to help, because it works at the sub-lexical level (but happily not exclusively at this level, as it retains its power once words begin to get fully formed, which is what we want). To do this, I used the venerable Brown Corpus, a fairly small (by today's standards) body of text containing about 1M words, which should be enough for this problem (note that I could have also used NLTK):CHAR_NGRAM_ORDER = 3 EPSILON = 1e-10 char_counts = defaultdict(int) for line in open('brown.txt'): words = re.sub(r'\W+', ' ', line).split() # tokenize with punctuation and whitespaces chars = ' '.join(words) char_counts[''] += len(chars) # this little hack is useful for 1-grams for n in range(CHAR_NGRAM_ORDER): for i in range(len(chars)): if i >= n: char_counts[chars[i-n:i+1]] += 1 # charProb('the') should be > than charProb('tha') def charProb(c): global char_counts if c in char_counts: return char_counts[c] / char_counts[c[:-1]] return EPSILON
The final required piece is the already mentioned function to compute the score for a given grid:
def gridScore(grid): # add spaces between rows s = ' '.join([''.join([grid[i][j] for i in range(19)]) for j in range(8)]) # tokenize with punctuation and whitespaces s = ' '.join(re.sub(r'\W+', ' ', s).split()) LL = 0 # log-likelihood for i in range(len(s)): probs = [] for n in range(CHAR_NGRAM_ORDER): if i >= n: probs.append(charProb(s[i-n:i+1])) # interpolated LMs with uniform weights pi = sum([p/len(probs) for p in probs]) LL += math.log(pi) return LL
So.. does this work? Not terribly well unfortunately.. Although with some tuning (the most important aspect being the order N of the model) it's possible to reach somewhat interesting states like this:
| i|nf|or|ma|ti|on|ed|Cl|au|de| S|ha|nn|on| f|ou|nd| | |
|as|is| o|f | | | b|th|eo|ry|, |wh|ic|h |is| t|he| | |
| m|od|el|s |an|d |ge|pr|ob|ab|il|is|ti|c |la|ng|ua| | |
|et|ho|ds| t|ha|t | m|of| t|he| c|od|e |br|ea|ki|ng| | |
| t|hi|s |pr|ob|le|ve|yo|u |wo|ul|d |us|e |to| s|ol|m,| |
|"A| M|at|he|ma|ti|d |wi|th| t|he| p|ap|er| t|it|le|ca|l |
|n,|" |pu|bl|is|he|io|Th|eo|ry| o|f |Co|mm|un|ic|at|d | |
| | | | | | | |in| t|hi|s |ye|ar|. | | | | | |
The Solution
Considering the jittery nature of my simplistic optimization function (although you prefer it to go up, there is no guarantee that it will always do), I pondered for a while about a backtracking mechanism, to no avail. The real next step is rather obvious: characters are probably not enough, the model needs to be augmented at the level of words. The character-based model should be doing most of the work in the first steps of the exploration (when the words are not fully formed), and the word-based model should take over progressively, as we zero in on the solution. It's easy to modify the previous code to introduce this new level:CHAR_NGRAM_ORDER = 6 WORD_NGRAM_ORDER = 1 char_counts = defaultdict(int) word_counts = defaultdict(int) for line in open('brown.txt'): # words words = re.sub(r'\W+', ' ', line).split() # tokenize with punctuation and whitespaces word_counts[''] += len(words) # this little hack is useful for 1-grams for n in range(WORD_NGRAM_ORDER): for i in range(len(words)): if i >= n: word_counts[' '.join(words[i-n:i+1])] += 1 # chars chars = ' '.join(words) char_counts[''] += len(chars) for n in range(CHAR_NGRAM_ORDER): for i in range(len(chars)): if i >= n: char_counts[chars[i-n:i+1]] += 1 # wordProb('table') should be > than wordProb('tabel') def wordProb(w): global word_counts words = w.split() h = ' '.join(words[:-1]) if w in word_counts: return word_counts[w] / word_counts[h] return EPSILON def gridScore(grid): # add spaces between rows s = ' '.join([''.join([grid[i][j] for i in range(19)]) for j in range(8)]) # tokenize with punctuation and whitespaces s = ' '.join(re.sub(r'\W+', ' ', s).split()) LL = 0 # log-likelihood for i in range(len(s)): probs = [] for n in range(CHAR_NGRAM_ORDER): if i >= n: probs.append(charProb(s[i-n:i+1])) if not probs: continue pi = sum([p/len(probs) for p in probs]) LL += math.log(pi) words = s.split() for i in range(len(words)): probs = [] for n in range(WORD_NGRAM_ORDER): if i >= n: probs.append(wordProb(' '.join(words[i-n:i+1]))) if not probs: continue pi = sum([p/len(probs) for p in probs]) LL += math.log(pi) return LL
And finally.. isn't it loopy in a strange way that the solution to a problem refers to what is probably the most efficient way of solving it?
That was really fun, as the rest of the course was, and if this could be of interest to anyone, the code is available on GitHub.