Or.. Some Variations on a Brute-Force Search Theme
While browsing for
code golfing ideas, I became interested in
Sudoku solving. But while by definition Sudoku code golfing is focused on source size (i.e. trying to come up with the smallest solver for language X, in terms of number of lines, or even characters), I was more interested in writing clear code, to hopefully learn a few insights on the problem.
Representational Preliminaries
I first came up with this Python class, to represent a Sudoku puzzle:
class Sudoku:
def __init__(self, conf):
self.grid = defaultdict(lambda: defaultdict(int))
self.rows = defaultdict(set)
self.cols = defaultdict(set)
self.boxes = defaultdict(set)
self.size = int(math.sqrt(len(conf))) for i in range(self.size): for j in range(self.size):
v = conf[(i * self.size) + j]
if v.isdigit():
self.set(i, j, int(v))
def set(self, i, j, v):
self.grid[i][j] = v
self.rows[i].add(v)
self.cols[j].add(v)
self.boxes[self.box(i, j)].add(v)
def unset(self, i, j):
v = self.grid[i][j]
self.rows[i].remove(v)
self.cols[j].remove(v)
self.boxes[self.box(i, j)].remove(v)
self.grid[i][j] = 0
def isValid(self, i, j, v):
return not (v in self.rows[i] or
v in self.cols[j] or
v in self.boxes[self.box(i, j)])
def box(self, i, j):
if self.size == 9:
return ((i // 3) * 3) + (j // 3)
elif self.size == 8:
return ((i // 2) * 2) + (j // 4)
elif self.size == 6:
return ((i // 2) * 2) + (j // 3)
assert False, 'not implemented for size %d' % self.size
The puzzle is initialized with a simple configuration string, for instance:
easy = "530070000600195000098000060800060003400803001700020006060000280000419005000080079"
harder = "..............3.85..1.2.......5.7.....4...1...9.......5......73..2.1........4...9"
and it can actually fit Sudoku variants of different size: 9x9, 8x8, 6x6. The only thing that changes for each is the definition of the
box method for finding the "coordinates" of a box, given a square position.
Validity Checking
One interesting aspect to note about this implementation is the use of a series of
set data structures (for rows, columns and boxes, wrapped in
defaultdicts, to avoid the initialization step), to make the validation of a "move" (i.e. putting a value in a square) more efficient. To be a valid move (according to Sudoku rules), the value must not be found in the corresponding row, column or box, which the
isValid method can tell very quickly (because looking for something in a set is efficient), by simply checking that it is not in any of the three sets. In fact many Sudoku code golf
implementations, based on a single list representation (rather than a two-dimensional grid), use a clever and compact trick for validity checks (along the lines of):
for i in range(81):
invalid_values_for_i = set()
for j in range(81):
if j / 9 == i / 9 or j % 9 == i % 9 or ((j / 27 == i / 27) and (j % 9 / 3) == (i % 9 / 3)):
invalid_values_for_i.add(grid_as_list[j])
valid_values_for_i = set(range(1, 10)) - invalid_values_for_i
which you'll find, after having scratched your head for a while, that although it does indeed work... is actually less efficient, because it relies on two imbricated loops looking at all elements (hence is in O(size
2)), whereas my technique:
for i in range(9):
for j in range(9):
valid_values_for_ij = [v for v in range(1, 10) if self.isValid(i, j, v)]
by exploiting the set data structure, actually runs slightly faster, in O(size
1.5).
Sequential Solver
With all that, the only piece missing is indeed a solver. Although there are many techniques that try to exploit human-style deduction rules, I wanted to study the less informed methods, where the space of possible moves is explored, in a systematic way, without relying on complex analysis for guidance. My first attempt was a brute-force solver that would simply explore the available moves, from the top left of the grid to the bottom right, recursively:
def solveSequentially(self, i=0, j=0):
solved = False
while self.grid[i][j] and not solved:
j += 1
if j % self.size == 0:
i += 1
j = 0
solved = (i >= self.size)
if solved:
return True
for v in range(1, self.size+1):
if self.isValid(i, j, v):
self.set(i, j, v)
if self.solveSequentially(i, j):
return True
self.unset(i, j)
return False
This solver is not terribly efficient. To see why, we can use a simple counter that is incremented every time the solver function is called: 4209 times for the "easy" puzzle (above), and a whopping 69,175,317 times for the "harder" one! Clearly there's room for improvement.
Random Solver
Next I wondered how a random solver (i.e. instead of visiting the squares sequentially, pick them in any order) would behave in comparison:
def solveRandomly(self):
self.n_calls += 1
available_ijs = []
for i in range(self.size):
for j in range(self.size):
if self.grid[i][j]: continue
available_ijs.append((i, j))
if not available_ijs:
return True
i, j = random.choice(available_ijs)
opts_ij = []
for v in range(1, self.size+1):
if self.isValid(i, j, v):
opts_ij.append(v)
for v in opts_ij:
self.set(i, j, v)
if self.solveRandomly():
return True
self.unset(i, j)
return False
This is really worst... sometimes by many orders of magnitude (it is of course variable). I'm not sure I fully understand why, because without thinking much about it would seem that it is not any more "random" than the sequential path choosing of the previous method. My only hypothesis is that the sequential path choosing works best because it is row-based: a given square at position (
i,
j) benefits from a previous move made at (
i,
j-1), because the additional constraint directly applies to it (as well as to all the other squares in the same row, column or box), by virtue of the Sudoku rules. Whereas with random choosing, it is very likely that this benefit will be lost, as the solver keeps randomly jumping to possibly farther parts of the grid.
Greedy Solver
While again studying the same code golf
implementations, I noticed that they're doing another clever thing: visiting first the squares with the
least number of possible choices (instead of completely ignoring this information, as the previous methods do). This sounded like a very reasonable heuristic to try:
def solveGreedily(self):
nopts = {}
for i in range(self.size):
for j in range(self.size):
if self.grid[i][j]: continue
opts_ij = []
for v in range(1, self.size+1):
if self.isValid(i, j, v):
opts_ij.append(v)
nopts[len(opts_ij)] = (opts_ij, (i,j))
if nopts:
opts_ij, (i,j) = min(nopts.items())[1]
for v in opts_ij:
self.set(i, j, v)
if self.solveGreedily():
return True
self.unset(i, j)
return False
return True
Performance is way better with this one: only 52 calls for the easy problem, and 10903 for the hard one. This strategy is quite simple: collect all the possible values associated to every squares, and visit the one with the minimum number (without bothering for ties). However, even though this solver clearly performs better, it's important to note that a single call (i.e. for a particular square) is now less efficient, because it has to look at every square, to find the one with the fewest choices (whereas the sequential solver didn't have to choose, as the visiting order was fixed). This is the price to pay for introducing a little more wisdom in our strategy, but there are however two easy ways we can speed things up (not in terms of number of calls this time, but rather in terms of overall efficiency): first, whenever we find a square with no possible choice, we can safely back up right away (right in the middle of the search), because we can be sure that this is not a promising configuration. Second, whenever we find a square with only one choice, we can stop the search and proceed immediately with the result just found, because the minimum is what we are looking for anyway. Applying those two ideas, the solver then becomes:
def solveGreedilyStopEarlier(self):
nopts = {}
single_found = False
for i in range(self.size):
for j in range(self.size):
if self.grid[i][j]: continue
opts_ij = []
for v in range(1, self.size+1):
if self.isValid(i, j, v):
opts_ij.append(v)
n = len(opts_ij)
if n == 0: return False
nopts[n] = (opts_ij, (i,j))
if n == 1:
single_found = True
break
if single_found:
break
if nopts:
opts_ij, (i,j) = min(nopts.items())[1]
for v in opts_ij:
self.set(i, j, v)
if self.solveGreedilyStopEarlier():
return True
self.unset(i, j)
return False
return True
But a question remains however (at least for me, at this point): why does it work? To better understand, let's study a very easy 6x6 puzzle:
s = "624005000462000536306000201050005000"
6 2 4 | . . 5
. . . | 4 6 2
--------+--------
. . . | 5 3 6
3 . 6 | . . .
--------+--------
2 . 1 | . 5 .
. . 5 | . . .
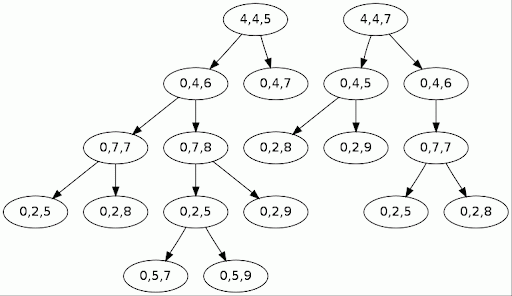
First, here is the exploration path taken by the sequential solver (read from left to right; each node has the square's
i and
j coordinates, as well as its chosen value):
In contrast, here is the path taken by the greedy solver:
Whenever the solver picks the right answer for a certain square, the remaining puzzle becomes more constrained, hence simpler to solve. Picking the square with the minimal number of choices minimizes the probability of an error, and so also minimizes the time lost in wrong path branches (i.e. branches that cannot lead to a solution). The linear path shown above is an optimal way of solving the problem, in the sense that the solver never faces any ambiguity: it is always certain to make the good choice, because it follows a path where there is only one, at each stage. This can also be seen on this harder 9x9 problem:
s = "120400300300010050006000100700090000040603000003002000500080700007000005000000098"
1 2 . | 4 . . | 3 . .
3 . . | . 1 . | . 5 .
. . 6 | . . . | 1 . .
---------+-----------+---------
7 . . | . 9 . | . . .
. 4 . | 6 . 3 | . . .
. . 3 | . . 2 | . . .
---------+-----------+---------
5 . . | . 8 . | 7 . .
. . 7 | . . . | . . 5
. . . | . . . | . 9 8
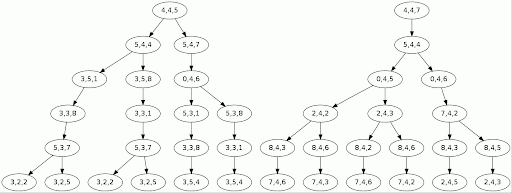
with which the sequential solver has obviously a tougher job to do (read from top to bottom; only the 6 first recursion levels are shown):
But even though its path is not as linear as with simpler puzzles (because ambiguity is the defining feature of harder problems), the greedy solver's job is still without a doubt less complicated:
This last example shows that our optimized solver's guesses are not always the right ones: sometimes it needs to back up to recover from an error. This is because our solver employs a
greedy strategy, able to find efficiently an optimal solution to a wide variety of problems, which unfortunately doesn't include Sudoku. Because it is equivalent to a
graph coloring problem, which is
NP-complete, there is in fact little hope of finding a truly efficient strategy. Intuitively, the fundamental difficulty of the problem can be seen if you imagine yourself at a particular branching path node, trying to figure out the best way to go. There is nothing there (or from your preceding steps) that can tell you, without a doubt, which way leads to success. Sure you can guide your steps with a reasonable strategy, as we did, but you can never be totally sure about it, before you go there and see by yourself. But sometimes by then, it is too late, and you have to go back...
Preventing Unnecessary Recursion
The last thing I wanted to try was again inspired from the code golfing
ideas cited above: for the moves with only one possible value, why not try to avoid recursion altogether (note that although the poster suggests this idea, I don't see it actually implemented in any of the code examples, at least not the way I understand it). Combining it with the previous ideas, this one can be implemented like this:
def solveGreedilyStopEarlierWithLessRecursion(self):
single_value_ijs = []
while True:
nopts = {}
single_found = False
for i in range(self.size):
for j in range(self.size):
if self.grid[i][j]: continue
opts_ij = []
for v in range(1, self.size+1):
if self.isValid(i, j, v):
opts_ij.append(v)
n = len(opts_ij)
if n == 0:
for i, j in single_value_ijs:
self.unset(i, j)
return False
nopts[n] = (opts_ij, (i,j))
if n == 1:
single_found = True
break
if single_found:
break
if nopts:
opts_ij, (i,j) = min(nopts.items())[1]
if single_found:
self.set(i, j, opts_ij[0])
single_value_ijs.append((i,j))
continue
for v in opts_ij:
self.set(i, j, v)
if self.solveGreedilyStopEarlierWithLessRecursion():
return True
self.unset(i, j)
for i, j in single_value_ijs:
self.unset(i, j)
return False
return True
The single-valued moves are now handled in a
while loop (with a properly placed
continue statement), instead of creating additional recursion levels. The only gotcha aspect is the additional bookkeeping needed to "unset" all the tried single-valued moves (in case there were many of them, chained in the
while loop) at the end of an unsuccessful branch (just before both places where
False is returned). Because of course a single-valued move is not guaranteed to be correct: it may be performed in a wrong branch of the exploration path, and thus needed to be undone, when the solver backs up. This technique is interesting, as it yields a ~85% improvement on the problem above, in terms of number of calls. Recursion could of course be totally dispensed with, but I suspect that this would require some important changes to the problem representation, so I will stop here.
This ends my study of some brute-force Sudoku solving strategies. I will now take some time to look at some more refined techniques, by some famous people:
Peter Norvig's constraint propagation strategy, and
Donald Knuth's Dancing Links.
The code in this article can be found on my
GitHub.